(3x3+13x2-13x+2): (x-1)=
En primer lugar colocamos los coeficientes del dividendo en un fila. En este caso el polinomio es completo, si no fuera así completaría con ceros, 0.
(3x3+13x2-13x+2): (x-1)=
Posteriormente, colocamos el opuesto (le cambiamos el signo) del termino independiente del divisor.
(3x3+13x2-13x+2): (x–1)=
Para empezar, bajamos el primer coeficiente.
Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
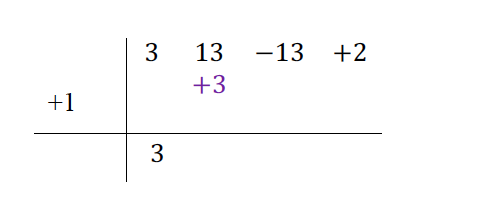
Sumamos los dos coeficientes.
Repetimos el proceso anterior y vamos completando paso a paso la tabla.
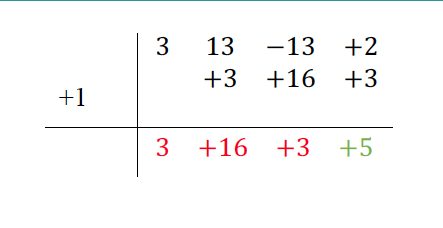Aquí, debemos tener en cuenta que:
Así: C(x)=3x2+16x+3 y R(x)=5
Para entender mejor este tema se presenta el siguiente enlace donde están algunos ejemplos y practicas para que entiendan mejor el tema:
https://ekuatio.com/la-regla-de-ruffini/
Además; el link de una aplicacion donde se puede realizar este caso:
https://www.geogebra.org/m/YadfrN42
Finalmente, un vídeo para afianzar el contenido:
( ) ( )
2. Se coloca “x^n” como primer término en ambos paréntesis
(x^n ) (x^n )
3. Multiplicamos el signo del primer término del trinomio por el signo del segundo y lo colocamos después de la “x” del primer paréntesis. Hacemos lo mismo con el signo del segundo y del tercer término y lo ubicamos después de la “x” del segundo paréntesis
(x^n ± ) (x^n ± )
4. Buscamos dos números (que los llamaremos “p” y “q”)
Tiene que cumplir que
p + q = b y pq = c
es decir, que su suma dé “b” y su multiplicación dé “c”
se acomodan en los paréntesis poniendo el mayor en el primero, y quedaría
(x^n ± p ) (x^n ± q )
Ejemplo:
Buscamos dos números que sumados de 10 y multiplicados 24 , ésos son 4 y 6
Entonces nuestra factorización quedaría así:
Lo podemos probar multiplicando los binomios entre sí y reduciendo términos semejantes
Con el siguiente vídeo se va a entender mejor este tema:
Ejemplo:
1. Toda la expresión se multiplica y divide por el coeficiente del primer término. El primer término queda todo elevado al cuadrado ya que ambos , tanto “3” como “x” quedan elevados al cuadrado. El segundo término queda con “3” multiplicando a la “x”. Y el tercer término se multiplica por “3”
Noten que ahora en el numerador queda una expresión de la forma x^(2n)+bx^n+c con n=1 , el cual es el caso anterior de factorización y por lo tanto se sigue el mismo proceso para resolverlo
2. El numerador se factoriza como trinomio de la forma x^(2n)+bx^n+c . Se necesitan dos números que multiplicados den “15” y sumados den “8” . Éstos son “5” y “3”
3. Se factoriza el numerador por factor común con el fin de cancelar el denominador, que en este caso es “3” . Se factoriza (3x+3) , su factor común es 3 , y es precisamente lo que se necesita para cancelar el denominador
4. Se cancelan los “3’s” y queda:
Entonces la expresión factorizada quedaría:
Y además, una presentación en prezi para entender mejor.
https://prezi.com/hpxnl2eqxomo/factorizacion-de-trinomios-de-la-forma-ax2nbxnc/
Existen expresiones del tipo xn ± yn , por ejemplo x3 + 1, x5 – y5 , etc.
Primero debemos verificar si la expresión puede ser factorizada.
Para ello la igualamos a cero y resolvemos para una de sus variables. Si esto es posible entonces si se puede factorizar.
En el siguiente vídeo se puede observar como se resuelve de una manera mas explicativa:
Ejemplos: X5 – y5 , X5 – y5 = 0, X5 = y5 , x=y. Si se puede factorizar.
a4 + b4 , a4 + b4 = 0, a4 = -b4 . No es posible extraer raíz cuarta a un número negativo, por tanto no se puede factorizar.
La factorización de este tipo de expresiones es de la siguiente forma:
xn + yn = (x + y)(xn-1 – xn-2y + xn-3y2 ….- xyn-2 + yn-1)
xn – yn = (x - y)(xn-1 + xn-2y + xn-3y2 ….+ xyn-2 + yn-1)
Notas: El primer factor tiene la misma operación (suma o resta) de la expresión original.
Cuando la expresión original es una suma, los signos en el segundo factor son alternados empezando en positivo. Si la expresión original es una resta, los signos en el segundo factor son todos positivos.
Los exponentes de la primera variable van disminuyendo, mientras que los de la segunda variable van aumentando.
Ejemplos: Sea la expresión X5 – y5
Ya hemos verificado que es factorizable, por tanto continuamos con el proceso:
(x-y)(x4 – x3 y + x2 y 2 – xy3 + y4 )
La factorizacion de la diferencia de cuadrados perfectos es igual al producto de la suma por la diferencia de las raíces cuadradas de los términos. Es decir:
:
Ejemplo:
Para entender mejor el tema se presenta el siguiente enlace donde podrá encontrar más información sobre factorización de la diferencia de cuadrados perfectos y algunos ejercicios interactivos para practicar:
Y un vídeo donde se explica de mejor manera el tema:
EL ADIVINO. El Adivino es una fábula corta para niños. Forma parte de los cuentos de Esopo, un famoso escritor de fábulas que vivió en el...
