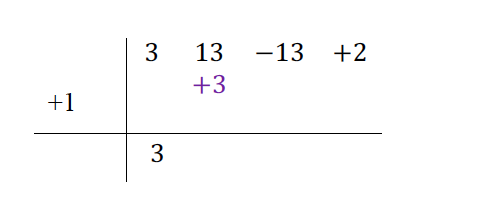Factorización de polinomios. Factor común.

Factorización de polinomios. Factor común.

Para entender este tema vamos a partir de lo que es factorizar un número que consiste en expresarlo como producto de sus factores. Si todos los términos de un polinomio tienen un factor común, se puede resolver con la aplicación de la propiedad distributiva esto nos permitirá expresar el polinomio como el producto de dos factores donde uno de ellos será el factor común.

Existen varias formas de factorizar polinomios por factor común expuestas a continuación: 

• Factor primo

Para factorizar un número como producto de sus factores primos se debe descomponer en factores primos.

Ejemplo: descomposición del número 60.

La descomposición en factores primos seria 2*2*3*5.

A continuación, se presenta un vídeo donde se explica un ejemplo de factor primo.

• Máximo común divisor

Para factorizar con el máximo común divisor se debe descomponer cada uno de los polinomios en factores primos, el M.C.D. es el producto de los factores comunes con su menor exponente.

Ejemplo:

Hallar el M.C.D de 12,18 y 20:

Primero se descomponen los números en factores primos.

12=2*2*3           18=2*3*3          20=2*2*5

El M.C.D entre (12,18,20) es 2

• Mínimo común múltiplo

Al igual que el anterior, se deben descomponer en factores primos; el m.c.m es el producto de todos los factores que aparecen elevados a los menores exponentes.

Ejemplo: 

Como en el anterior ejemplo descompusimos vamos a tomar los mismos términos entonces tenemos:

que el m.c.m de (12,18,20) es 2*2*3*3*5=180 

• Factor común de un polinomio

Para calcular el factor común de un polinomio se halla el M.C.D. de los coeficientes y se multiplica por el M.C.D de la parte literal.

Para poder afianzar este tema se va a incluir un enlace donde existen unos ejercicios y una explicación de lo que pueden practicar.

https://es.khanacademy.org/math/algebra-basics/alg-basics-quadratics-and-polynomials/alg-basics-factoring-polynomials-1-common-factors/a/taking-common-factors

Y un enlace de un vídeo donde pueden entender mejor la factorización de polinomios.

https://www.youtube.com/watch?v=0jyVQVanXfE

Factorización aplicando la regla de Ruffini

Factorización aplicando la regla de Ruffini

 El método de Ruffini fue descrito por el matemático, profesor y médico italiano Paolo Ruffini en el año de 1804, quien además de inventar el famoso método denominado regla de Ruffini, que ayuda a encontrar los coeficientes del resultado de la fracmentación de un polinomio por el binomio.

Esta técnica posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1. Y para que esto sea posible se necesita saber o conocer por lo menos una de las raíces del polinomio único, con el propósito de que la separación sea exacta.

Ejemplo:

(3x3+13x2-13x+2): (x-1)=

En primer lugar colocamos los coeficientes del dividendo en un fila. En este caso el polinomio es completo, si no fuera así completaría con ceros, 0.

(3x3+13x2-13x+2): (x-1)=

Posteriormente, colocamos el opuesto (le cambiamos el signo) del termino independiente del divisor.

(3x3+13x2-13x+2): (x–1)=

Para empezar, bajamos el primer coeficiente.

Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.

Sumamos los dos coeficientes.

Repetimos el proceso anterior y vamos completando paso a paso la tabla.

Aquí, debemos tener en cuenta que:

• El grado del cociente es una unidad inferior al grado del dividendo.
• El resto es siempre un número.

Así: C(x)=3x2+16x+3 y R(x)=5

Para entender mejor este tema se presenta el siguiente enlace donde están algunos ejemplos y practicas para que entiendan mejor el tema:

https://ekuatio.com/la-regla-de-ruffini/

Además; el link de una aplicacion donde se puede realizar este caso:

https://www.geogebra.org/m/YadfrN42

Finalmente, un vídeo para afianzar el contenido:

Factorización de trinomios de la forma x²^n + bx^n + c

Factorización de trinomios de la forma x²^n + bx^n  + c

Un trinomio de la forma  x²^n + bx^n  + c, con n como un número entero, es factorizable si existen dos números p y q que cumplen las condiciones p + q =  b y pq = c. En este caso, el trinomio se expresa como el producto de dos binomios con primer término x^n y como segundos términos los números p y q. Es decir: x²^n + bx^n  + c = (x^n + p)(x^n + q)

Para factorizar se debe tomar en cuenta los siguientes pasos:

1. Abrimos dos paréntesis multiplicándose entre sí

(            ) (            )

2.   Se coloca “x^n” como primer término en ambos paréntesis

(x^n       ) (x^n       )

3.   Multiplicamos el signo del primer término del trinomio por el signo del segundo y lo colocamos después de la “x” del primer paréntesis. Hacemos lo mismo con el signo del segundo y del tercer término y lo ubicamos después de la “x” del segundo paréntesis

(x^n ±      ) (x^n ±      )

4. Buscamos dos números (que los llamaremos “p” y “q”)

Tiene que cumplir que

p + q = b              y              pq = c

es decir, que su suma dé “b” y su multiplicación dé “c”

se acomodan en los paréntesis poniendo el mayor en el primero, y quedaría

(x^n ± p ) (x^n ± q )

Ejemplo:

Buscamos dos números que sumados de 10 y multiplicados 24 , ésos son 4 y 6

Entonces nuestra factorización quedaría así:

Lo podemos  probar multiplicando los binomios entre sí y reduciendo términos semejantes

Con el siguiente vídeo se va a entender mejor este tema:

TRINOMIO DE LA FORMA AX^(2N)+BX^N+C

trinomio de la forma AX^(2N)+BX^N+C

La fórmula para este case es la siguiente: 

Para realizar este tipo de factorización se debe tener en cuenta algunos puntos:

El coeficiente del primer término, el cual es “a”, siempre debe ser diferente a “1” , ya que si a=1 este caso sería exactamente igual al anterior, que es “x^(2n)+bx+c.

El exponente de la variable del primer término siempre debe ser el doble que el del segundo término.

El tercer término siempre será un término independiente, es decir, sin variable.

En el vídeo se explica mejor lo que es este caso:

Ejemplo:

 

1.   Toda la expresión se multiplica y divide por el coeficiente del primer término. El primer término queda todo elevado al cuadrado ya que ambos , tanto “3” como “x” quedan elevados al cuadrado. El segundo término queda con “3” multiplicando a la “x”. Y el tercer término se multiplica por “3”

Noten que ahora en el numerador queda una expresión de la forma x^(2n)+bx^n+c con n=1 , el cual es el caso anterior de factorización y por lo tanto se sigue el mismo proceso para resolverlo 

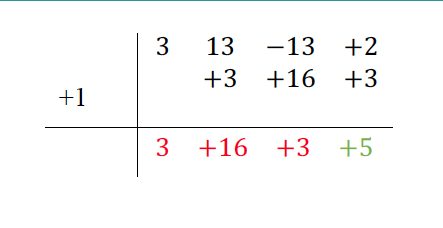
2.   El numerador se factoriza como trinomio de la forma x^(2n)+bx^n+c . Se necesitan dos números que multiplicados den “15” y sumados den “8” . Éstos son “5” y “3”

3.   Se factoriza el numerador por factor común con el fin de cancelar el denominador, que en este caso es “3” . Se factoriza (3x+3) , su factor común es 3 , y es precisamente lo que se necesita para cancelar el denominador

4.   Se cancelan los “3’s” y queda:

Entonces la expresión factorizada quedaría:

 Y además, una presentación en prezi para entender mejor.

https://prezi.com/hpxnl2eqxomo/factorizacion-de-trinomios-de-la-forma-ax2nbxnc/

Factorización de trinomios cuadrados perfectos

Factorización de trinomios cuadrados perfectos

El trinomio cuadrado perfecto es llamado así ya que el primer y  último término son cuadrados perfectos y el valor central equivale al doble del producto de las raíces cuadradas del primer y tercer término .

Para determinar si un trinomio es cuadrado perfecto se debe:

 1.- Identificar los dos términos que son cuadrados perfectos sacando  su raíz cuadrada.

 2.- Identificar si el tercer término corresponde al doble producto de la raíz cuadrada de los dos términos del punto anterior. 

Ejemplo:

Para afianzar el tema se presenta el siguiente vídeo

A continuación, se les presenta un link donde van a encontrar algunos ejercicios.

https://www.superprof.es/diccionario/matematicas/algebra/trinomio-perfecto.html

:

Trinomio cuadrado perfecto por adición y sustracción

Trinomio cuadrado perfecto por adición y sustracción  

Para que una expresión sea un trinomio cuadrado perfecto, se debe sumar y restar un mismo número  (semejante al segundo término) para que el segundo término sea el doble producto de las raíces cuadradas del primer y último término. A este proceso se le denomina completar cuadrados.

Ejemplo: m⁴ + 6m² + 25.

 

Para que m⁴ + 6m² + 25, sea un trinomio cuadrado perfecto, el segundo término debe ser igual a 10m². Por esto, se le debe sumar y restar al trinomio es 4m² , pues 6m² + 4m² = 10m²

 

Para factorizar un trinomio cuadrado perfecto por adición y sustracción, se completan cuadrados y se factoriza la expresión, primero como un trinomio cuadrado perfecto y después, como una diferencia de cuadrados.

En el siguiente vídeo se puede entender mejor este tema:

Para que puedan practicar sobre este tema se deja el siguiente enlace donde existe un juego interactivo sobre trinomio cuadrado perfecto por adición y sustracción.

https://quizizz.com/admin/quiz/5dd34c22cda2d8001bc03a87/trinomio-cuadrado-perfecto-por-adicion-y-sustraccion

Factorización de expresiones de la forma Xn±Yn

Factorización de expresiones de la forma Xn±Yn

    Existen expresiones del tipo xn ± yn , por ejemplo x3 + 1, x5 – y5 , etc. 

Primero debemos verificar si la expresión puede ser factorizada. 

Para ello la igualamos a cero y resolvemos para una de sus variables. Si esto es posible entonces si se puede factorizar. 

En el siguiente vídeo se puede observar como se resuelve de una manera mas explicativa:

Ejemplos: X5 – y5 , X5 – y5 = 0, X5 = y5 , x=y. Si se puede factorizar. 

a4 + b4 , a4 + b4 = 0, a4 = -b4 . No es posible extraer raíz cuarta a un número negativo, por tanto no se puede factorizar.

La factorización de este tipo de expresiones es de la siguiente forma:

 xn + yn = (x + y)(xn-1 – xn-2y + xn-3y2 ….- xyn-2 + yn-1)

 xn – yn = (x - y)(xn-1 + xn-2y + xn-3y2 ….+ xyn-2 + yn-1)

 Notas: El primer factor tiene la misma operación (suma o resta) de la expresión original. 

Cuando la expresión original es una suma, los signos en el segundo factor son alternados empezando en positivo. Si la expresión original es una resta, los signos en el segundo factor son todos positivos. 

Los exponentes de la primera variable van disminuyendo, mientras que los de la segunda variable van aumentando. 

Ejemplos: Sea la expresión X5 – y5 

Ya hemos verificado que es factorizable, por tanto continuamos con el proceso: 

(x-y)(x4 – x3 y + x2 y 2 – xy3 + y4 )

Factorización de cubos perfectos. Suma y diferencia

Factorización de cubos perfectos. Suma y diferencia

Factorización de la suma de cubos perfectos

La suma de cubos perfectos equivale al producto de dos factores: el primero, un binomio formado por las raíces cúbicas de los términos; el segundo, un trinomio cuyos términos son el cuadrado de la primera raíz menos el producto de las raíces más el cuadrado de la segunda raíz.

La factorización de la suma de cubos perfectos se expresa así:

  (x³+ y³ =(x + y)(x² - xy  + y² ) 

Ejemplo;

El siguiente vídeo le aportá información sobre resolución de  un ejercicio sobre el caso de factorización tratado. 

Factorización de la diferencia de cubos perfectos

 La diferencia de dos cubos perfectos equivale a multiplicar dos factores: el primero, un binomio formado por la diferencia de las raíces cúbicas de los términos; el segundo, un trinomio cuyos términos son el cuadrado de la primera raíz más el producto de las raíces más el cuadrado de la segunda raíz. 

La factorización de la diferencia de cubos perfectos se expresa así: 

 (x³- y³ =(x - y)(x² + xy  + y² ) 

Ejemplo:

El siguiente vídeo tiene como finalidad que usted pueda observar paso a paso la resolución de un ejercicio.

Factorización de la diferencia de cuadrados perfectos

Factorización de la diferencia de cuadrados perfectos

La factorizacion de la diferencia de cuadrados perfectos es igual al producto de la suma por la diferencia de las  raíces cuadradas de los términos. Es decir: 

Ejemplo explicativo:

:

Ejemplo:

Para entender mejor el tema se presenta el siguiente enlace donde podrá encontrar más información sobre factorización de la diferencia de cuadrados perfectos y algunos ejercicios interactivos para practicar:

https://es.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-difference-squares/a/factoring-quadratics-difference-of-squares 

Y un vídeo donde se explica de mejor manera el tema:

Factorización por Agrupación de Términos

                          Factorización por Agrupación de Términos 

Para factorizar un polinomio por agrupación de términos, se aplica la propiedad asociativa de la adición y la propiedad distributiva de la multiplicación con respecto a la adición. de esta manera se hallan factores comunes a cada grupo de términos.

Ejemplos:

Factorizar $3x^2+6x+4x+8$3, x, squared, plus, 6, x, plus, 4, x, plus, 8

$\begin{aligned}&\phantom{=}3x^2+6x+4x+8\\\\ &=(3x^2+6x)+(4x+8)&&\small{\gray{\text{Agrupa términos.}}}\\ \\ &=3x({x+2})+4({x+2})&&\small{\gray{\text{Factoriza los MCD.}}}\\ \\ &=3x(\goldD{x+2})+4(\goldD{x+2})&&\small{\gray{\text{¡Factor común!}}}\\\\ &=(\goldD{x+2})(3x+4)&&\small{\gray{\text{Factoriza } x+2.}} \end{aligned}$

La forma factorizada es $(x+2)(3x+4)$left parenthesis, x, plus, 2, right parenthesis, left parenthesis, 3, x, plus, 4, right parenthesis.

En el siguiente enlace encontrará más ejemplos  sobre el tema tratado, y actividades que le ayudarán a su aprendizaje.

http://es.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-quadratics-grouping/a/factoring-by-grouping